Viet Nguyen, Giang Vu, Tung Nguyen Thanh, Khoat Than, Toan Tran
Introduction
With the advance of deep learning, many visual recognition tasks such as image classification [3], object detection [7], and semantic segmentation [6] have achieved great performances. However, deep learning methods typically require a large set of labeled data for training deep neural networks. Such large datasets are difficult and time-consuming to collect and annotate for many tasks.
Learning with limited supervision is a key challenge to translate research efforts of deep neural networks to real-world applications where large-scale annotated datasets are prohibitively costly to acquire. This issue has motivated the recent topic of few-shot learning (FSL), which aims to build a system that can quickly learn new tasks from a small number of labeled data.
Recent approaches for few-shot learning can roughly be grouped into two categories corresponding to two most important components of a few-shot model.
- Representation. The studies of this category focus on training a strong feature extractor on the base dataset. Typically, they adopt a standard supervised training procedure for the meta-training stage and fine-tunes a simple classifier (e.g. cosine similarity based classifier, logistic regression) with the limited supervision in the support set.
- Classifier. Given a well-trained representation, this approach tries to build a complex classifier that best fits the novel data. The classifiers of this category typically require an episodic training procedure that simulates the few-shot tasks by generating support sets and query sets from the base classes.
The two approaches are complementary and orthogonal to each other and can be combined to significantly improve the performance. In this blog post, we pay more attention to the second approach and propose a simple paradigm that utilizes samples of distractor classes along with support (and query) samples to fine-tune the classifier.
Learning with Counter-example
Humans learn new concepts in context – where we have already had prior knowledge about other entities. According to mental models in cognitive science, when assessing the validity of an inference, one would retrieve counter-examples, which do not lead to the conclusion despite satisfying the premise [1,2,4,5,8]. Thus, if there exists at least one of such counter-examples, the inference is known to be erroneous.
Hence, we attempt to equip few-shot learning with the above ability so that it can eliminate incorrect hypotheses when learning novel tasks in a data-driven manner. Specifically, we leverage out-of-distribution data, i.e. samples belonging to classes separated from novel tasks as counter-examples for preventing the learned prototypes from overfitting to their noisy features. To that end, when learning novel tasks, we adopt the large margin principle in metric learning [9] to encourage the learned prototypes to be close to support data while being far from out-of-distribution samples.

For instance, given limited supervision in support data, it is possible to have multiple explanations on a query sample, with each corresponding to a different prediction. Inductive bias allows the learner to systematically favor one explanation over another, rather than favoring a model that overfits to the limited support data. Figure 1 shows an ambiguous classification example that can be explained by multiple hypotheses. Two decision rules possibly learnt from the support data are:
- Suits belong to class 1; or
- Men belong to class 1.
Both rules are simple, but they can lead to completely different decisions for classifying the given query sample. However, it is unclear which rule the learner would favor; it is only possible to know after training. Hence, solely learning with support data can be obscure.
One way to narrow down the hypothesis space is using counter-examples to assess the inductive validity [4,1]. In figure 1, the out-of-distribution (OOD) sample of a dog wearing a suit, which plays as a counter example, hints that the suit should be considered irrelevant, and hence the rule 1 should be rejected.
Propose Approach
We introduce our novel technique for few-shot learning namely Penalizing Out-Of-Distribution SampLEs (POODLE). Specifically, we attempt to regularize few-shot learning and improve the generalization of the learned prototypes of the distance based classifier by leveraging prior knowledge of in- and out-of-distribution samples.
Our definition is as follows. Positive samples are in-distribution samples provided in the context of the current task that includes both support and query samples. Negative samples, by contrast, do not belong to the context of the current task, and hence are out-of-distribution. Negative samples can either provide additional cues that reduce ambiguity, or act as distractors to prevent the learner from overfitting.
Note that negative samples should have the same domain as positive samples so that their cues are insightful to the learner, but positive and negative samples are not required to have the same domain as the base data.
To effectively use positive and negative samples in few-shot learning, the following conditions must be met:
- The regularization guided by out-of-distribution samples can be combined with traditional loss functions for classification;
- The regularization should be applicable for both inductive and transductive inference; and
- Negative samples should be easily available for training.
The requirement on negative data should be minimal i.e. does not need any sort of labels except for aforementioned conditions.
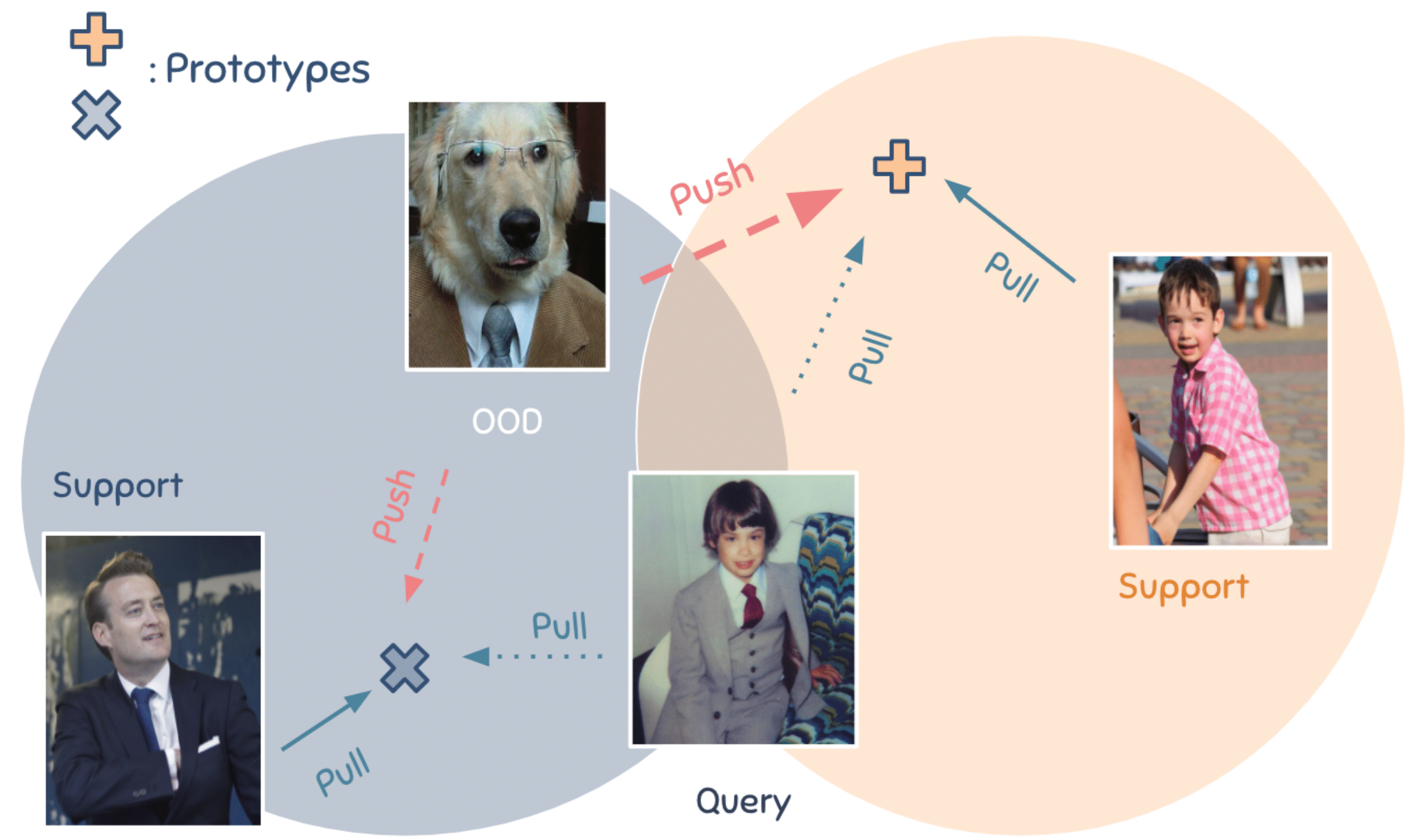
To this extent, we leverage the large-margin principle as in Large Margin Nearest Neighbors (LMNN) [9]. In these works, Weinberger et al. propose a loss function with two competing terms to learn a distance metric for nearest neighbor classification: a “pull” term to penalize the large distance between the embeddings of two nearby neighbors, which likely belong to the same class, and a “push” term to penalize the small distance between the embeddings of samples of difference classes.
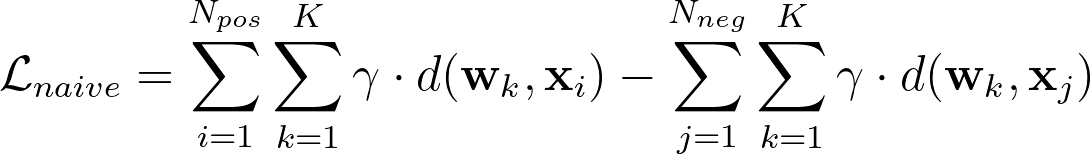
However, this objective does not take into account class assignments for positive samples. To tackle this problem, we use weighted distances between prototypes and samples to simultaneously optimize both objectives:
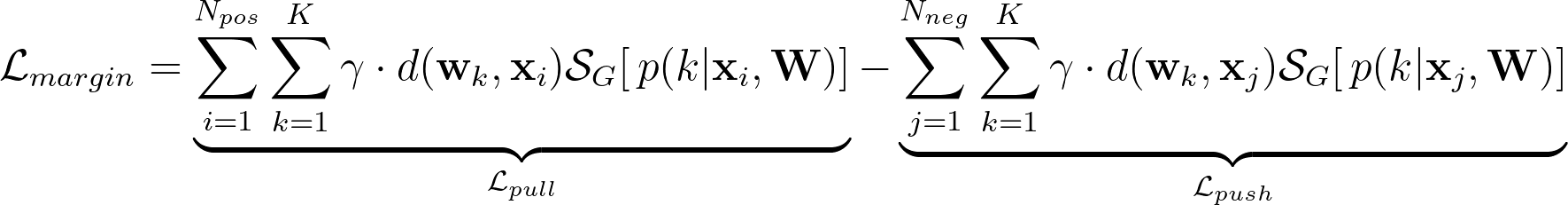
In summary, POODLE optimizes the classifier on novel tasks with the following objectives.
where Lce is the standard cross-entropy loss on support sample; Lpull is the “pull” term to pull prototypes close to the in-distribution data; Lpush is the “push” term to push prototypes far from the out-of-distribution data. The intuitive goal is minimizing distances from positive samples to prototypes, while maximizing distances from negative samples to prototypes.
Experiments
We conduct extensive experiments to demonstrate the performance gain of our method on standard inductive, transductive, cross-domain FSL. To demonstrate the robustness of our method across datasets/network architectures, we keep the hyperparameters fixed for all experiments.
As mentioned earlier, we focus on fine-tuning the classifier while leaving the feature extractor intact. We adopt three different training methods on the widely-used ResNet-12, namely Simple, Rot, and Rot+KD. They are combinations of supervised learning, self supervised learning and knowledge distillation. More details are described in the paper. Our method consistently improves over the cross-entropy counterpart on the three baselines.
Inductive
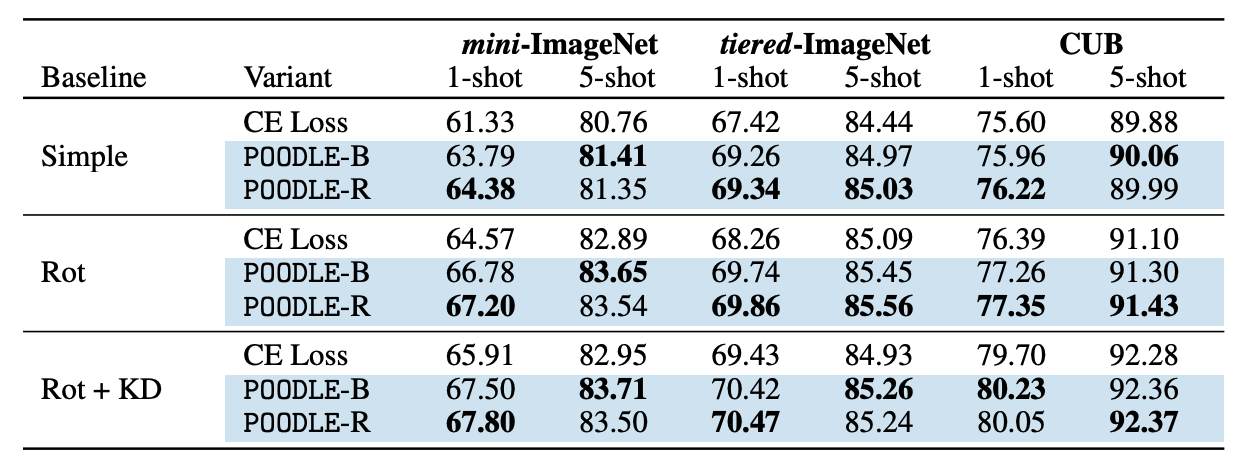
Table 1
Table 1 shows the results of our approach with various baselines with the inductive inference (positive samples are support images). As can be seen, our approach consistently boosts the performance of all baselines by a large margin (1-3%).
Transductive
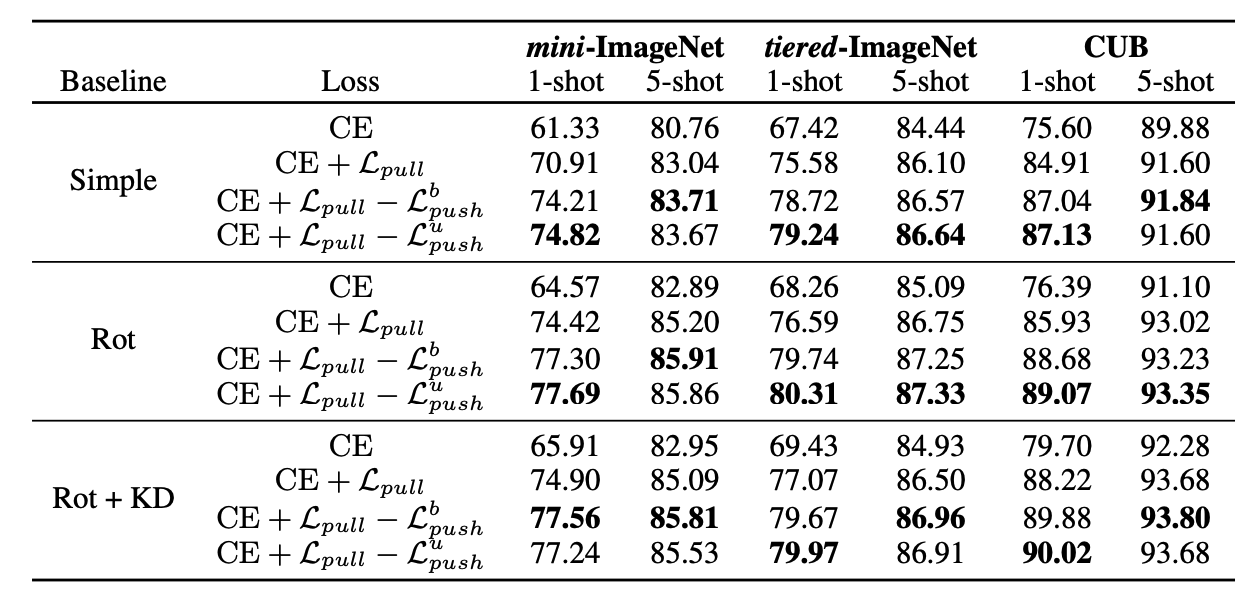
Table 2
Table 2 demonstrates the efficacy of each loss term of POODLE in transductive inference (positive samples are support and query images). We can see that using the “pull” loss with query samples improves the inductive baseline significantly, being as effective as other transductive algorithms. Combined with the “push” term, the classifier is further enhanced.
Comparisons with Previous Works
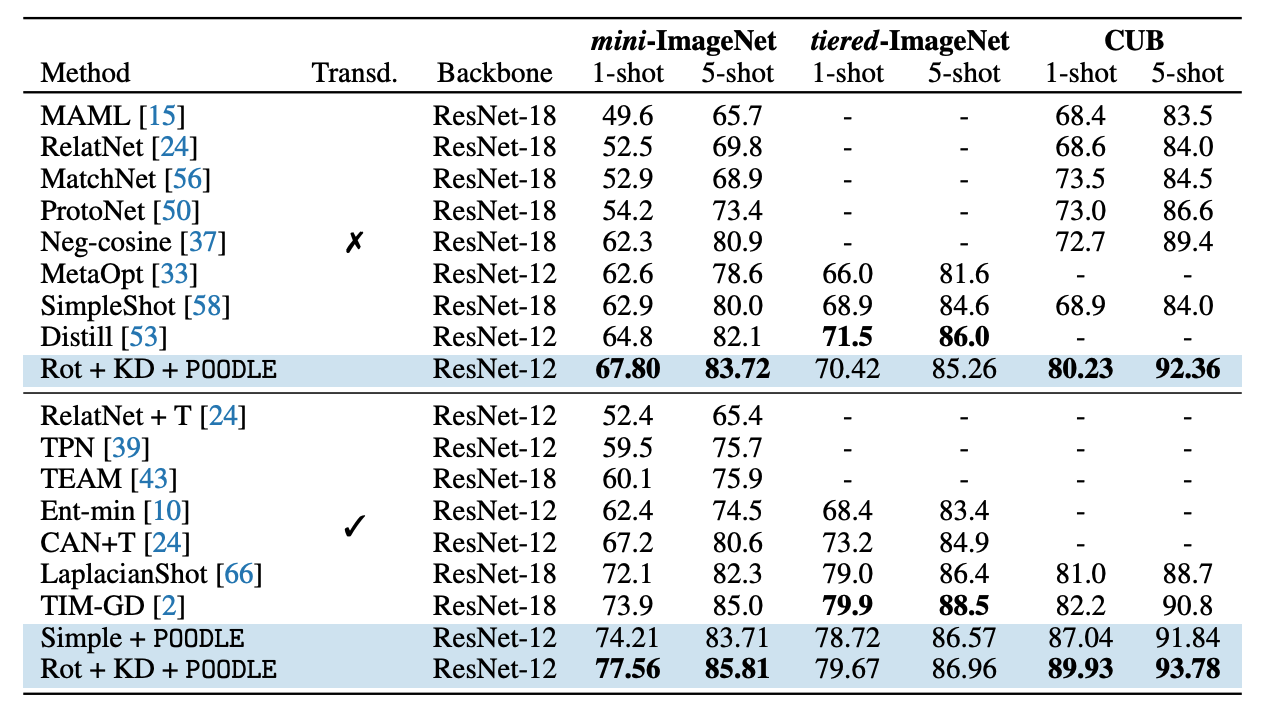
Table 3
At the time of submitting, our method achieved state-of-the-art on most of the standard benchmarks of few-shot learning. We report the performance of our network in comparison with state-of-the-art methods in both transductive and inductive settings (with and without information from the query images) in table 3. We can see that our approach remarkably improves the performance of the baselines and achieves a comparable performance with the state-of-the-art approaches in the tiered-ImageNet. In mini-ImageNet and CUB we significantly outperform the prior works in both inductive and transductive settings.
Conclusion
In this work, we have proposed the concept of leveraging out-of-distribution samples set to improve the generalization of few-shot learners and realize it by a simple yet effective objective function. Our approach consistently boosts the performance of FSL across different backbone networks, inference types (inductive/transductive), and the challenging cross-domain FSL.
Future work might seek to exploit different sampling strategies (ie how to select negative samples) to further boost the performance and reduce time/memory complexity; another interesting direction is enhancing the robustness of the classifier when we have both positive and negative samples in the same sampling pool; leveraging domain adaptation to reduce the need of in-domain negative samples is also a promising research direction.
References
- [1] Wim De Neys, Walter Schaeken, and Géry d’Ydewalle. Working memory and everyday con-ditional reasoning: Retrieval and inhibition of stored counterexamples. Thinking & Reasoning,11(4):349–381, 2005.
- [2] Dorothy Edgington. On conditionals. Mind, 104(414):235–329, 1995.
- [3] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 770–778, 2016.
- [4] Philip N Johnson-Laird. Mental models and human reasoning. Proceedings of the National Academy of Sciences, 107(43):18243–18250, 2010.
- [5] Philip Nicholas Johnson-Laird. Mental models: Towards a cognitive science of language, inference, and consciousness. Number 6. Harvard University Press, 1983.
- [6] Jonathan Long, Evan Shelhamer, and Trevor Darrell. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 3431–3440, 2015.
- [7] Joseph Redmon, Santosh Divvala, Ross Girshick, and Ali Farhadi. You only look once: Unified, real-time object detection. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 779–788, 2016.
- [8] Niki Verschueren, Walter Schaeken, and Gery d’Ydewalle. Everyday conditional reasoning: A working memory—dependent tradeoff between counterexample and likelihood use. Memory & Cognition, 33(1):107–119, 2005.
- [9] Kilian Q Weinberger, John Blitzer, and Lawrence K Saul. Distance metric learning for large margin nearest neighbor classification. In Advances in neural information processing systems, pages 1473–1480, 2006.
NeurIPS 2021: POODLE: Improving Few-shot Learning via Penalizing Out-of-Distribution Samples
Authors: Duong H. Le*, Khoi D. Nguyen*, Khoi Nguyen, Quoc-Huy Tran, Rang Nguyen, Binh-Son Hua
Overall
Le Hoang Duong, Nguyen Duc Khoi
Share Article




