Viet Nguyen, Giang Vu, Tung Nguyen Thanh, Khoat Than, Toan Tran
Improving Relational Regularized Autoencoders with Spherical Sliced Fused Gromov Wasserstein
Problem
Generative autoencoders have been widely used in various problems because of its ability to capture the data distribution and provide low-dimensional representation of the data. In this work, we enhance the performance of a class of generative autoencoders which is called relational regularized autoencoders by introducing new relational regularizations. In greater detail, we develop a new family of optimal transport discrepancies that plays the role as the latent regularization in the autoencoder framework.
Related work
The current state-of-the-art relational regularized autoencoders, deterministic relational regularized autoencoders (DRAE) [1], relies on the usage of sliced fused Gromov Wasserstein (SFG) [1]. The key idea is to incorporate relational comparison between the distribution of the encoded data and the mixture of Gaussians prior distribution. Despite the fact that the DRAE has an appealing quality in practice, it does not exploit the full potential of the relational regularization. In particular, the SFG underestimates the discrepancy between two distributions due to the uniform slicing method. Using uniform distribution over slicing directions is treating all directions the same, which is an unrealistic assumption in the context of big data (low-dimensional manifold hypothesis) [2].
- [1] H. Xu, D. Luo, R. Henao, S. Shah, and L. Carin. Learning autoencoders with relational regularization. arXiv preprint arXiv:2002.02913, 2020
- [2] I. Deshpande, Y.-T. Hu, R. Sun, A. Pyrros, N. Siddiqui, S. Koyejo, Z. Zhao, D. Forsyth, and A. G. Schwing. Max-sliced Wasserstein distance and its use for GANs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 10648–10656, 2019
The proposed method
To address the previous concern, we replace the uniform distribution by different distributions over projecting directions (the unit-hypersphere). First, we propose to use the von-Mises Fisher distribution (see Figure 1) for capturing the most informative area of directions with controllable size. The optimization is choosing the location parameter of the von-Mises Fisher distribution that can maximize the 1D fused Gromov Wasserstein cost using the reparametrization trick and the sampling procedure of the von-Mises Fisher distribution.
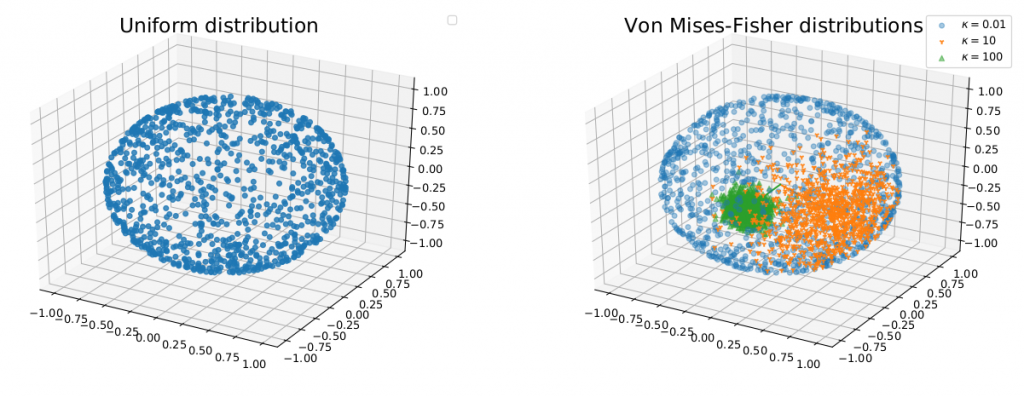
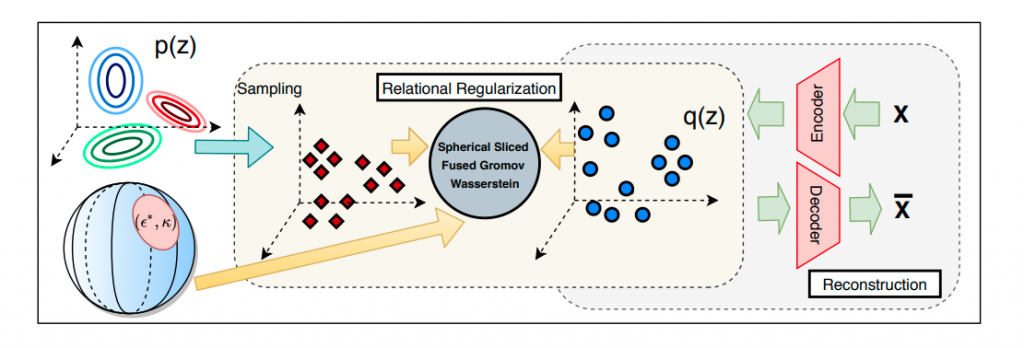
By doing so, we derive the spherical sliced fused Gromov Wasserstein (SSFG) discrepancy which is further proved as a pseudo metric in the space of probability distributions. Similar to the SFG, the SSFG has a fast computational speed and does not suffer from the curse of dimensionality. Moreover, the SSFG is the generalization and the interpolation between the SFG and its straight-forward extension, max-SFG. We apply the SSFG to the RAE framework to obtain a new type of autoencoder which is spherical DRAE (s-DRAE). Training the s-DRAE is minimizing the reconstruction loss of images and the SSFG between the latent code distribution and the mixture Guassian prior (see Figure 2).
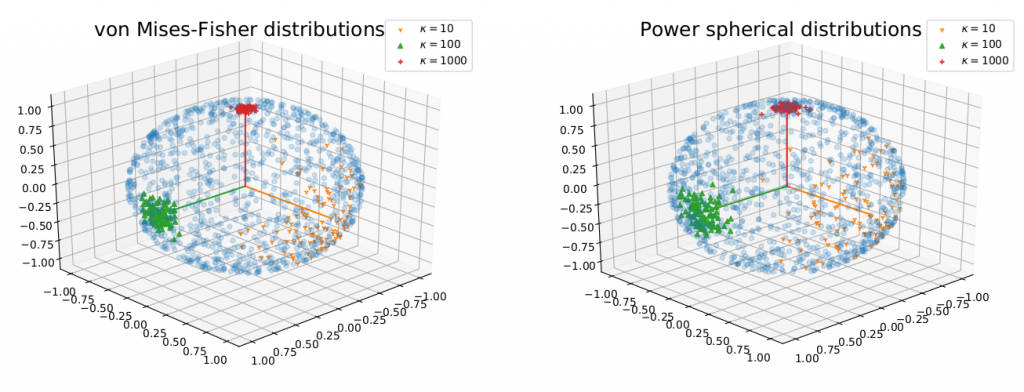
Another improvement to the SFG is to use the power spherical distribution as the slicing distribution. The power spherical distribution (see Figure 3) has similar properties as the von-Mises Fisher distribution however it has a faster and stabler sampling procedure. The application of the power spherical leads to a new divergence, power spherical sliced fused Gromov Wasserstein (PSSFG) and power spherical DRAE (ps-DRAE). We can show that the PSSFG has all properties of the SSFG and a faster computational time than the SSFG.
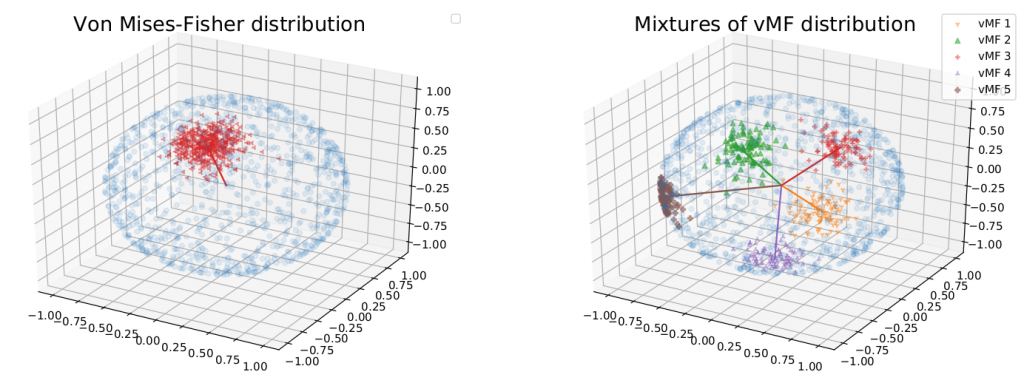
Finally, we further extend the family of discrepancies by utilizing the mixture of von-Mises Fisher (see Figure 4) (similar with the mixture of power spherical) to capture multiple areas of informative slicing directions. Hence, we are able to develop two new corresponding RAE which are mixture spherical DRAE (ms-DRAE) and mixture power spherical DRAE (mps-DRAE).
Empirical results
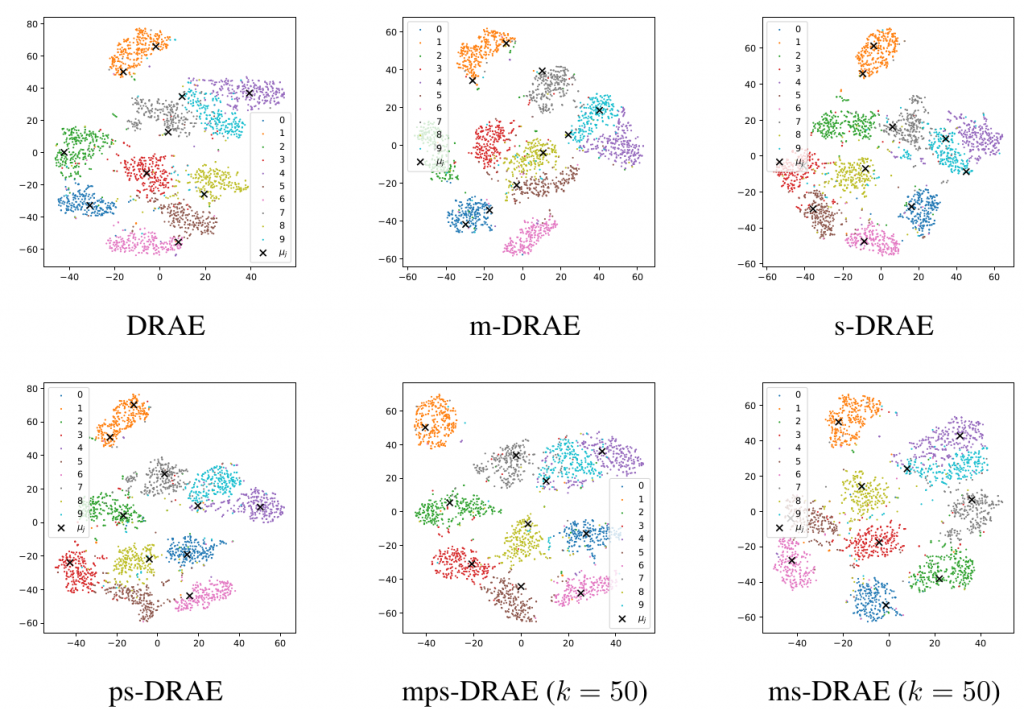
We compare the generative performance and reconstructive performance of our proposed autoencoders with standard generative autoencoders including probabilistic autoencoders and deterministic autoencoders. The experiments are conducted on two standard datasets which are the MNIST dataset and the CelebA dataset. First, we illustrate the FID score (lower is better) and reconstruction score (lower is better) in Table 1. We can see that our RAEs have better or at least comparable performance compared to other types of autoencoders.
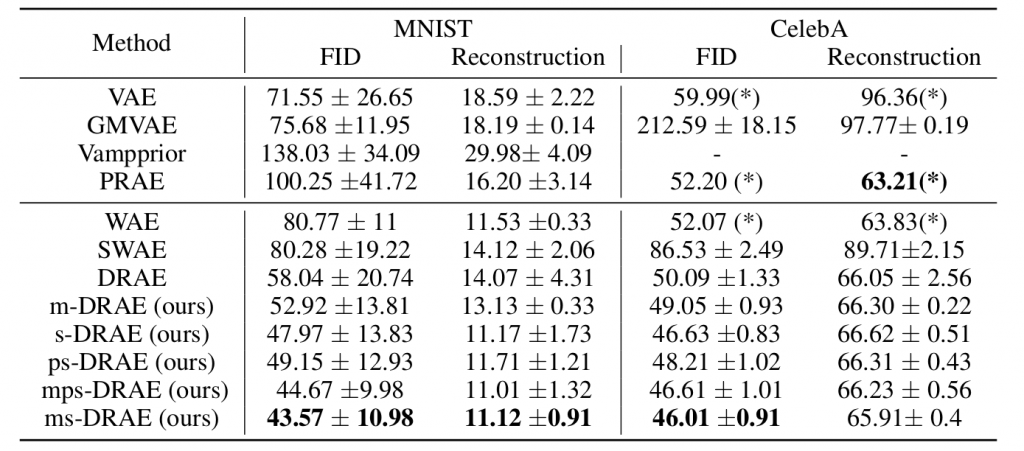
Finally, we show the latent visualization of autoencoders on the MNIST dataset in Figure 5 and some generated images on the CelebA dataset in Figure 6. Through these figures, it is easy to see that our proposed RAEs provide an appealing performance on learning latent manifolds and generating new images.

ICLR 2021 Poster: Improving Relational Regularized Autoencoders with Spherical Sliced Fused Gromov Wasserstein
Authors: Khai Nguyen, Son Nguyen, Nhat Ho, Tung Pham, Hung Bui
Overall
Khai Nguyen (VinAI Research Resident)
Share Article




