Viet Nguyen, Giang Vu, Tung Nguyen Thanh, Khoat Than, Toan Tran
Introduction
Deep learning has become a revolution with many tremendous successes impacting comprehensively on the fields of both scientific research and application. Although it has significantly advanced the state of the art in terms of the predictive accuracy of various tasks, deep neural networks still suffer from several critical limitations regarding uncertainty estimates, robustness, and adaptability. Bayesian neural networks (BNNs) have been promoted to address these problems.
Bayesian principle for deep learning models offers a probabilistic interpretation for deep learning models by imposing a prior distribution on the weight parameters and aiming to obtain a posterior distribution instead of only point estimates. However, exactly computing the posterior of non-linear high-dimensional BNNs is infeasible and approximate inference has been devised. The core question posed is how to construct an expressive approximation for the true posterior while maintaining computational efficiency and scalability, especially for modern deep learning architectures. Our work proposes a novel solution to tackle this challenge.
Motivation
From the literature, the typical mean-field variational inference [1] is favorable in analytical calculation and implementation. However, it ignores the strong dependencies among random weights of neural nets, which is usually inefficient to capture the complicated structure of the true posterior and also to estimate the true model uncertainty. There are many extensive studies proposed to provide posterior approximations with richer representation such as low-rank Gaussian and variants [7], matrix or implicit distributions [5,6], etc. They significantly improve both predictive accuracy and uncertainty calibration, but some methods incur a large computational complexity and are difficult to integrate into convolutional layers.
We, on the other hand, focused on another line of work called Dropout Variational Inference (DVI) [2,3], which interprets Dropout regularization in deterministic neural networks as a form of approximate inference in Bayesian deep models. In practice, DVI has shown competitive performances in terms of predictive accuracy on various tasks, even compared to the structured Bayesian approximation, but with much cheaper computational complexity. We further realized the distinctiveness of DVI is that it could rationally acquire the complementary benefits of Bayesian inference and theoretical Dropout inductive biases [9]. So, we have believed that the Dropout principle would offer several potentials to improve approximate inference in Bayesian deep networks.
With the above inspiration, we investigated the limitations of DVI frameworks, of which we noticed that these methods also employed the simple structures of mean-field family and their approximations often fail to obtain satisfactory uncertainty estimates [8]. Therefore, we came up with a natural idea that: “a richer representation for the noise distribution would enrich the expressiveness of Dropout posterior via the Bayesian interpretation”. However, we encountered three non-trivial challenges when implementing this idea:
- How to maintain the backpropagation in parallel and optimize efficiently with gradient-based methods (as the vanilla Dropout procedures)
- DVI has a bottleneck called “KL-condition” which restricts the form of both the prior and approximate posterior [2,3], and
- DVI based on multiplicative Gaussian noise suffers from theoretical pathologies, including using improper prior leading to ill-posed true posterior, and singularity of the approximate posterior making the variational objective undefined [4].
We propose a novel structured variational inference framework named “Variational Structured Dropout” (VSD) to address all these challenges.
The Proposed Approach
Given a deterministic neural net with the weight parameter Θ of size K x Q. Consider training this model with multiplicative Dropout procedure, in which the Dropout noise is sampled from a diagonal Gaussian distribution:
with α is the droprate vector of size K. Our method adopts an orthogonal approximation called Householder transformation to learn a structured representation for the multiplicative Gaussian noise.
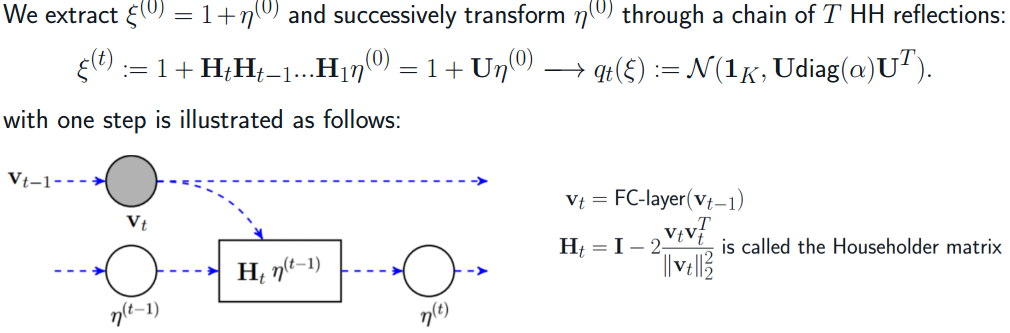
Fig. 1: One step of the Householder transformation
As a consequence of the Bayesian interpretation, we go beyond the mean-field family and obtain a variational Dropout posterior with structured covariance. We use variational inference with structured posterior approximation qt(W) and optimize the variational lower bound as follows:
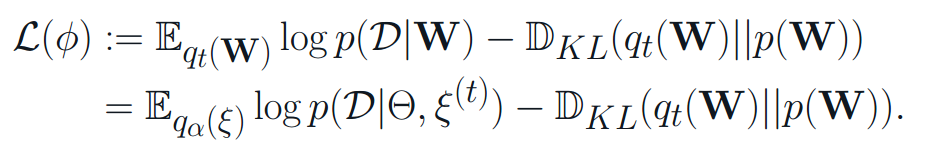
Overcoming the singularity issue of approximate posterior: In Variational Dropout (VD) [2] method using multiplicative diagonal noise, there is a mismatch in support between the approximate posterior and the prior, thus making the KL term undefined. Specifically, the approximate distribution always assigns all its mass on subspaces defined by the directions aligned with the rows of Θ. These subspaces have Lebesgue measure zero causing the singularities in approximate posterior, and the KL term will be undefined whenever the prior p(W) puts zero mass to these subspaces.
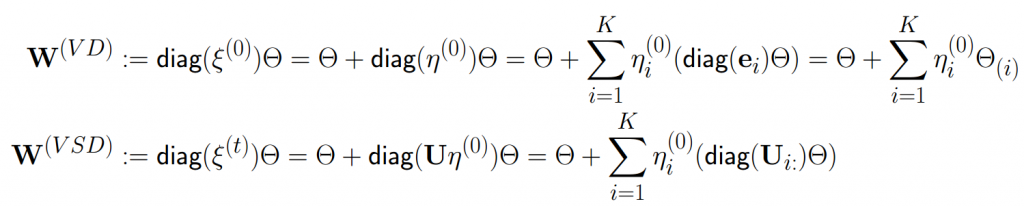
However, in VSD the scalar noises are not treated separately due to the structured correlation, namely VSD would injects each ξi into the whole matrix Θ instead of some individual directions. In other words, VSD maintains a trainable orthogonal matrix U which prevents the approximate posterior from having degenerate supports with measure zero, thereby avoiding the singularity issue.
Derivation of tractable variational objective:

From the information-theoretic perspective, augmenting the mutual information is a standard principle for structure learning in Bayesian networks. Particularly in our derivation, maximizing the alternative objective LMI(φ) would help to sustain the dependence structure between columns of the network weights regardless of the factorized structure of prior distribution. Interestingly, this technique is utilized reasonably in our method. This is because our dependence structure allows us to specify explicitly the marginal distribution on each column of W, leading to a tractable objective whose KL divergence between two multivariate Gaussian can be calculated analytically in closed-form. We note that a similar application to other structured approximations, such as low-rank, Kroneckerfactored, or matrix variate Gaussian, can be non-trivial.
Experiments
We conducted extensive experiments with standard datasets and different network architectures to validate the effectiveness of our method on many criteria, including scalability, predictive accuracy, uncertainty calibration, and out-of-distribution detection.
Some related works: Monte Carlo Dropout (MCD, ICML16), Variational Dropout (VD, NeurIPS15), Bayes by Backprop (BBB, ICML15), Deep Ensemble (DE, NeurIPS17), SWAG (NeurIPS19), ELRG (NeurIPS20).
Computational complexity:
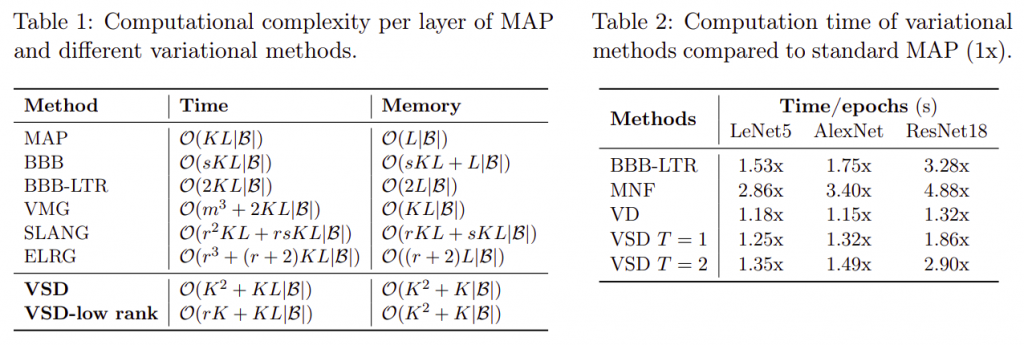
Results of image classification task:
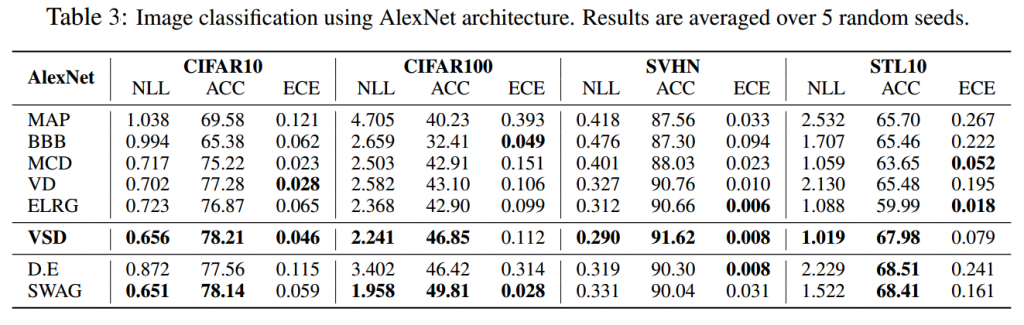
Predictive entropy performance:
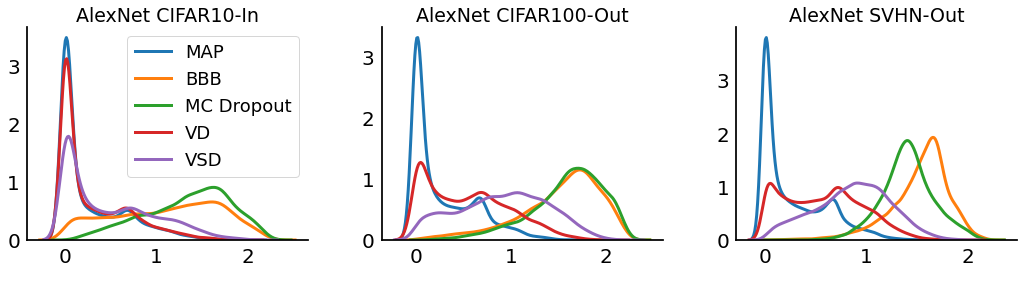
Fig. 2: Histogram of predictive entropies for AlexNet (top) and ResNet18 (bottom) trained on CIFAR10 and CIFAR100 respectively.
We train AlexNet model on CIFAR10 dataset and then consider out-of-distribution data from CIFAR100 and SVHN. The results show that the entropy densities of MAP and VD are concentrated excessively. This indicates that these methods could tend to make overconfident predictions on out-of-distribution data. Meanwhile, we observe the underconfident predictions of BBB and MC Dropout even on in-distribution data. In contrast, VSD is well-calibrated with a moderate level of confidence for in-distribution data and provides higher uncertainty estimates for out-of-distribution data.
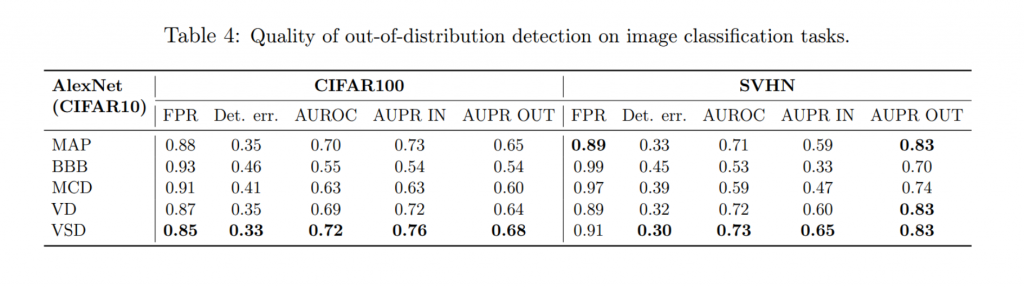
Out-of-distribution detection:
Conclusion
We proposed a novel approximate inference framework for Bayesian deep nets, named Variational Structured Dropout (VSD). In VSD, we learn a structured approximate posterior via the Dropout principle. VSD is able to yield a flexible inference while maintaining computational efficiency and scalability for deep convolutional models. The extensive experiments have evidenced the advantages of VSD such as well-calibrated prediction, better generalization, good uncertainty estimation. Given a consistent performance of VSD as presented throughout the paper, an extension of that method to other problems, such as Bayesian active learning or continual learning, is of interest.
References
[1] Charles Blundell, Julien Cornebise, Koray Kavukcuoglu, and Daan Wierstra. Weight uncertainty in neural networks. In International Conference on Machine Learning (ICML), 2015.
[2] Durk P Kingma, Tim Salimans, and Max Welling. Variational dropout and the local reparameterization trick. In Advances in Neural Information Processing Systems (NeurIPS), 2015.
[3] Yarin Gal and Zoubin Ghahramani. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning. In International Conference on Machine Learning (ICML), 2016.
[4] Jiri Hron, Alex Matthews, and Zoubin Ghahramani. Variational Bayesian dropout: Pitfalls and fixes. In International Conference on Machine Learning (ICML), 2018.
[5] Christos Louizos, Max Welling. Structured and efficient variational deep learning with matrix gaussian posteriors. In International Conference on Machine Learning (ICML), 2016.
[6] Christos Louizos and Max Welling. Multiplicative normalizing flows for variational Bayesian neural networks. In International Conference on Machine Learning (ICML), 2017.
[7] Aaron Mishkin, Frederik Kunstner, Didrik Nielsen, Mark Schmidt, and Mohammad Emtiyaz Khan. SLANG: Fast structured covariance approximations for Bayesian deep learning with natural gradient. In Advances in Neural Information Processing Systems (NeurIPS), 2018.
[8] Andrew Y. K. Foong, David R. Burt, Yingzhen Li, and Richard E. Turner. On the Expressiveness of Approximate Inference in Bayesian Neural Networks. In Advances in Neural Information Processing Systems (NIPS), 2020.
[9] Colin Wei, Sham Kakade, Tengyu Ma. The implicit and explicit regularization effects of dropout. In International Conference on Machine Learning (ICML), 2020.
Overall
Son Nguyen – Research Resident
Share Article




