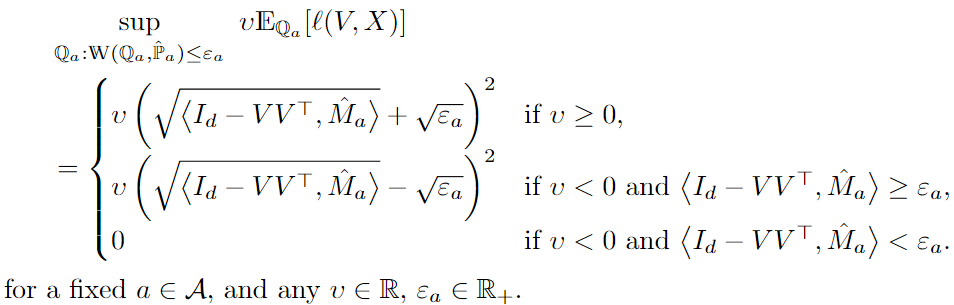Viet Nguyen, Giang Vu, Tung Nguyen Thanh, Khoat Than, Toan Tran
Introduction
Machine learning models are ubiquitous in our daily lives and supporting the decision-making process in diverse domains. With their flourishing applications, there also surface numerous concerns regarding the fairness of the models’ outputs (Mehrabi et al., 2021). Indeed, these models are prone to biases due to various reasons. It can be the demographic disparities in the data caused by the biases in data acquisition process or the imbalance of observed events at a specific period of time; or the data-driven characteristic of machine learning models; or the bias in human feedback to the predictive models which is the result of biased systems. Real-world examples of machine learning models that amplify biases and hence potentially cause unfairness are commonplace, ranging from recidivism prediction giving higher false positive rates for African-American to facial recognition systems having large error rate for women.
Various fairness criteria have been proposed to tackle the unfairness problem and due to the increasing demand of machine learning models to adapt to different scenarios in real life, it also requires that the fairness criteria are flexible and widely adopted as well.
Motivation
Strategies to mitigate algorithmic bias are investigated for all stages of the machine learning pipelines (Berk et al., 2021), i.e. at pre-processing steps, while training methods and at post-processing steps. However, most of them are for supervised learning scenarios, which encourage the (conditional) independence of the model’s predictions on a particular sensitive attribute.
We want to deal with this bias problem as early as possible then we focus on Principal Component Analysis (PCA), a fundamental dimensionality reduction technique that is widely used in the early stage of the machine learning pipelines (Pearson, 1901; Hotelling, 1933) and for unsupervised scenarios.
Different fairness criteria have been proposed to solve unfairness problems while learning a PCA model. Samadi et al. (2018) and Zalcberg & Wiesel (2021) propose to find the principal components that minimize the maximum subgroup reconstruction error; the min-max formulations can be relaxed and solved as semidefinite programs. However, the relaxation formulation can lead to unsatisfactory results and the solution may require additional dimensions to satisfy the fairness constraint. Olfat & Aswani (2019) propose to learn a transformation that minimizes the possibility of predicting the sensitive attribute from the projected data. However, their criterion is designed for a fixed family of classifiers and still resort to use a relaxation formulation of the original problem.
Furthermore, we also focus on the robustness criteria for the linear transformation. Recently, it has been observed that machine learning models are susceptible to small perturbations of the data. Distributionally robust optimization emerges as an useful tool for boosting the robustness of a machine learning model and has been shown to deliver promising out-of-sample performance in many applications ( Kuhn et al., 2019; Rahimian & Mehrotra, 2019; Nguyen et al. (2019)).
This work blends the ideas from the field of fairness in artificial intelligence and distributionally robust optimization.
Principal Component Analysis (PCA)
Given a sample , a projection matrix
with columns are orthonormal vectors, the reconstruction error is defined as:
With an empirical data distribution associated with
samples, the problem of PCA can be formulated as a stochastic optimization problem as follows:
It is well-known that PCA admits an analytical solution given by any orthonormal matrix whose columns are the eigenvectors associated with the largest eigenvalues of the sample covariance matrix.
Fair Principal Component Analysis
In the fair PCA setting, we are given a discrete sensitive attribute , where
may represent features such as race, gender or education. We consider a binary attribute
and let
.
We first introduce a novel unfairness penalty as the absolute difference between the conditional loss between two subgroups:
which is then incorporated into the original PCA objective:![]()
where is a penalty parameter to encourage fairness.
Distributionally Robust Fair PCA
We propose a robustified version of aforementioned Fair PCA optimization problem:
where we try to minimize the worst-case of the objective function over an ambiguity set ,
which is defined as follows:

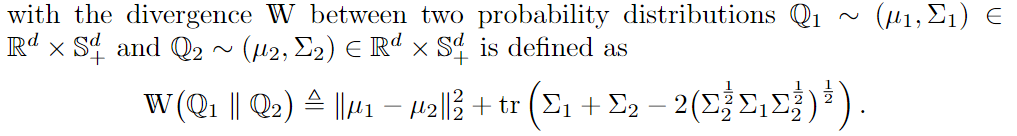
Reformulation
With the above distributionally robust fair PCA, we reformulate it as a weakly-convex optimization problem over the Stiefel manifold.
By expanding the definition of the unfairness penalty and the ambiguity set, we come up with computing the following term, which has analytical form under some mild conditions:
Then we can reformulate the full optimization problem as follows:
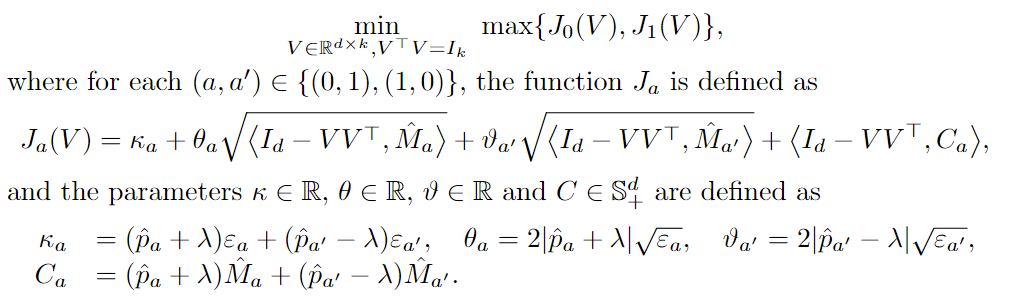 We further make the objective function convex by changing variable from
We further make the objective function convex by changing variable from to its complement
which satisfies
, then we have:
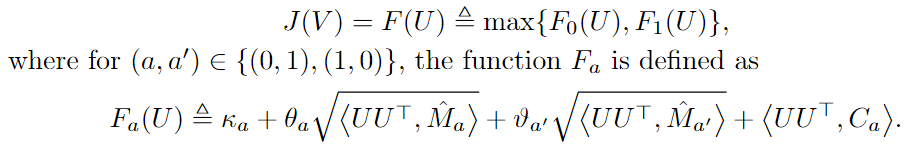
Finally, we have a convex optimization problem over the Stiefel manifold :
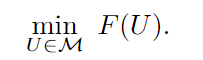
which can be solved by a Riemannian optimization algorithm (Absil et al., 2007).
Riemannian Subgradient Descents
We now can directly apply the Riemannian subgradient descent algorithm for the above optimization problem. Following the framework in Li et al. (2021), we first need to compute the subgradient , which is the orthogonal projection of the usual Euclidean subgradient onto the tangent space of the manifold
at the point
. As the point updated by gradient signal
may not lie on the manifold in general (
is the gradient signal,
is a step size) , we need an extra operation called “retraction” to project it back onto the manifold. Roughly speaking, the retraction operation
approximates the geodesic curve through
along the input tangential direction. The full algorithm is as follows:
which provides a sub-linear convergence rate:
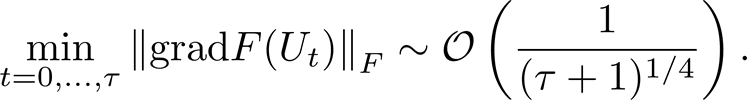 Experiments
Experiments
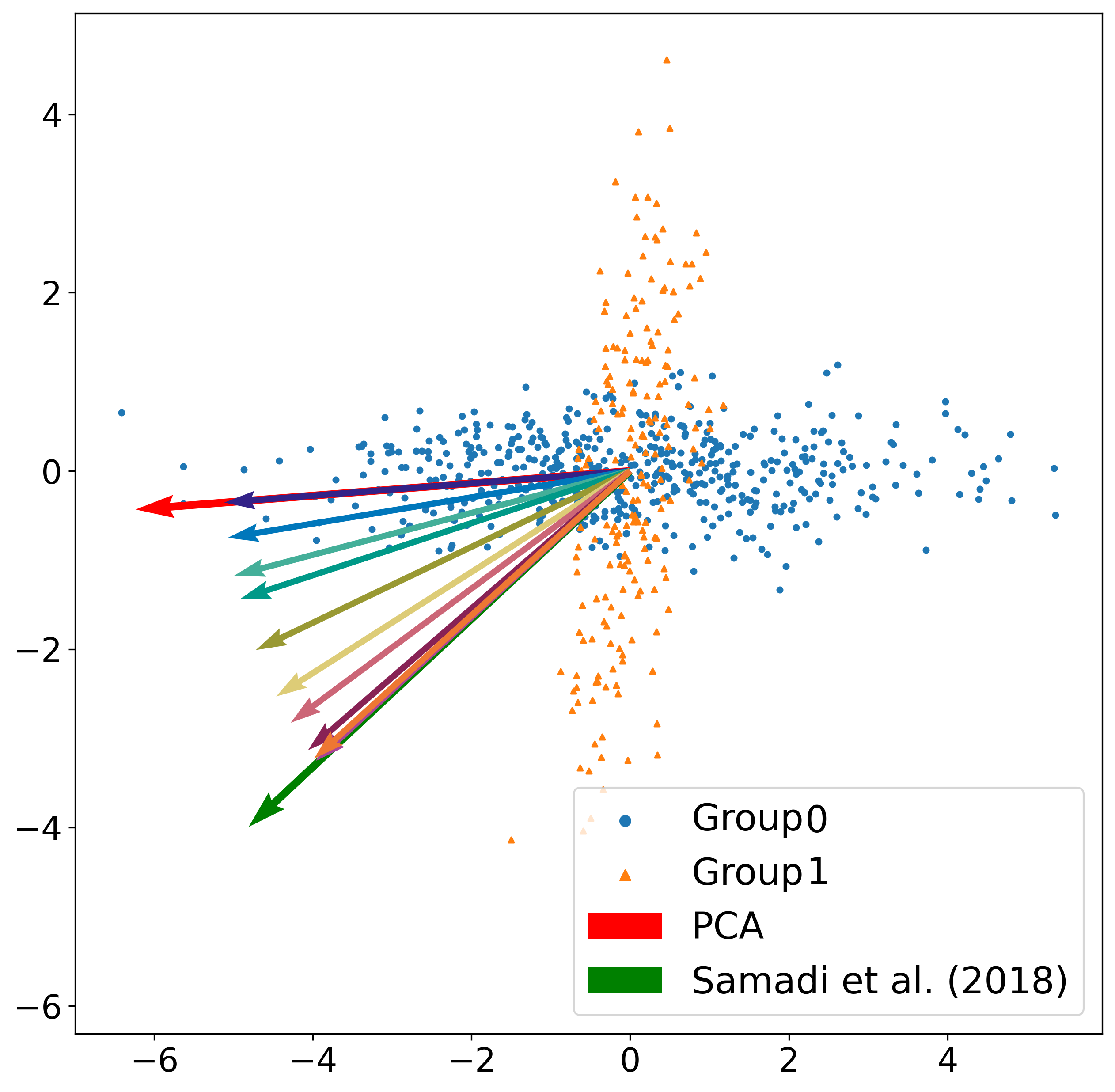
We first demonstrate the flexibility of our method on a 2-dimensional toy dataset, in which our method can recover the solution of the original PCA method, the solution of a fair PCA method, and cover the solution spectrum between the two solutions by sweeping over our penalization parameters appropriately. The results are demonstrated in the following figure:
We demonstrate the efficacy of our method by comparing it with two state-of-the-art Fair PCA methods over an extensive number of datasets. We evaluate methods over two criteria: the absolute difference between average reconstruction error between groups (ABDiff.), average reconstruction error of all data (ARE.). To emphasize the generalization capacity of each algorithm, we split each dataset into a training set and a test set with ratio of 30%-70% respectively, and only extract the top three principal components from the training set. We find the best hyper-parameters by 3-fold cross validation, and prioritize the one giving the minimum value of the summation (ABDiff.+ARE.). The results are averaged over 10 different training-testing splits.
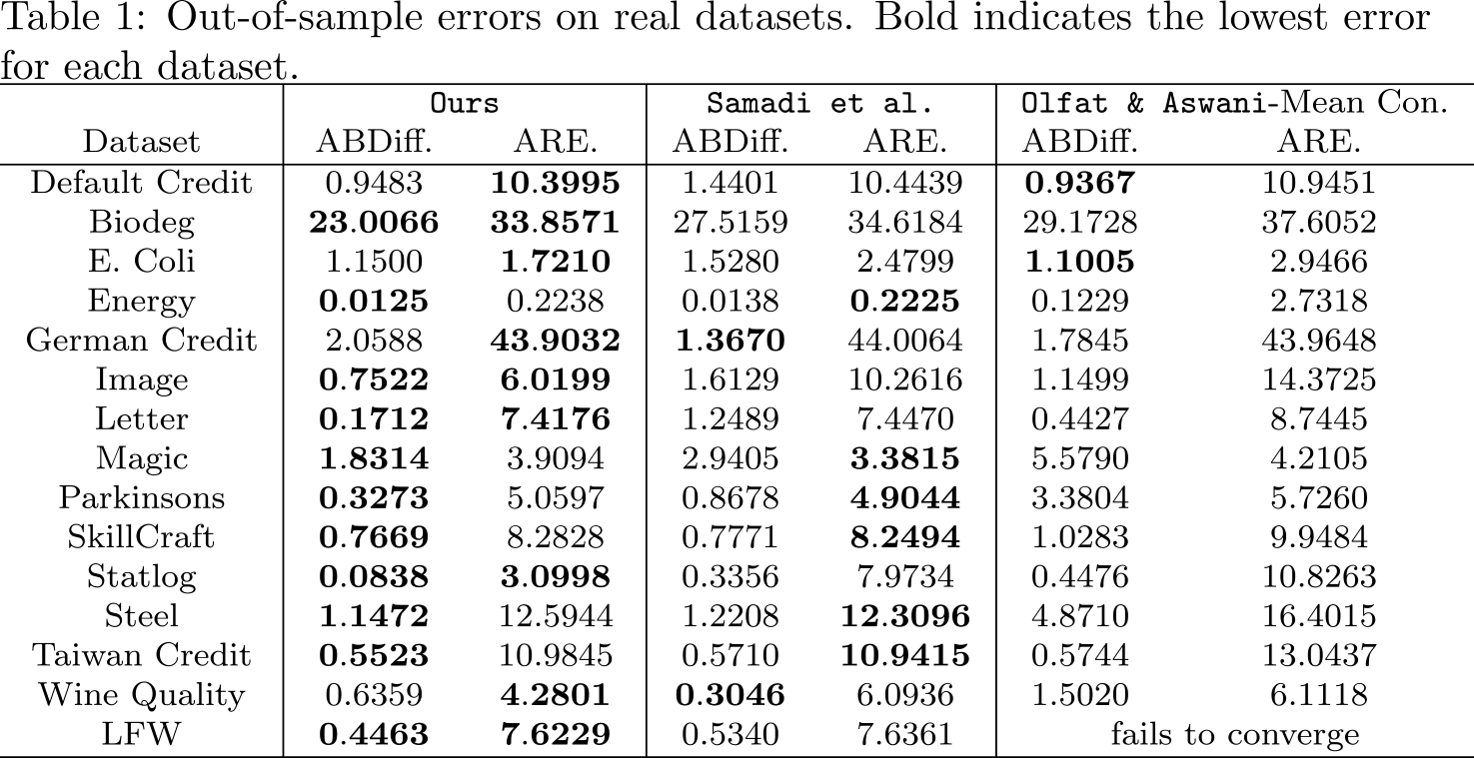
Our proposed method outperforms on the majority of the datasets in both criteria.
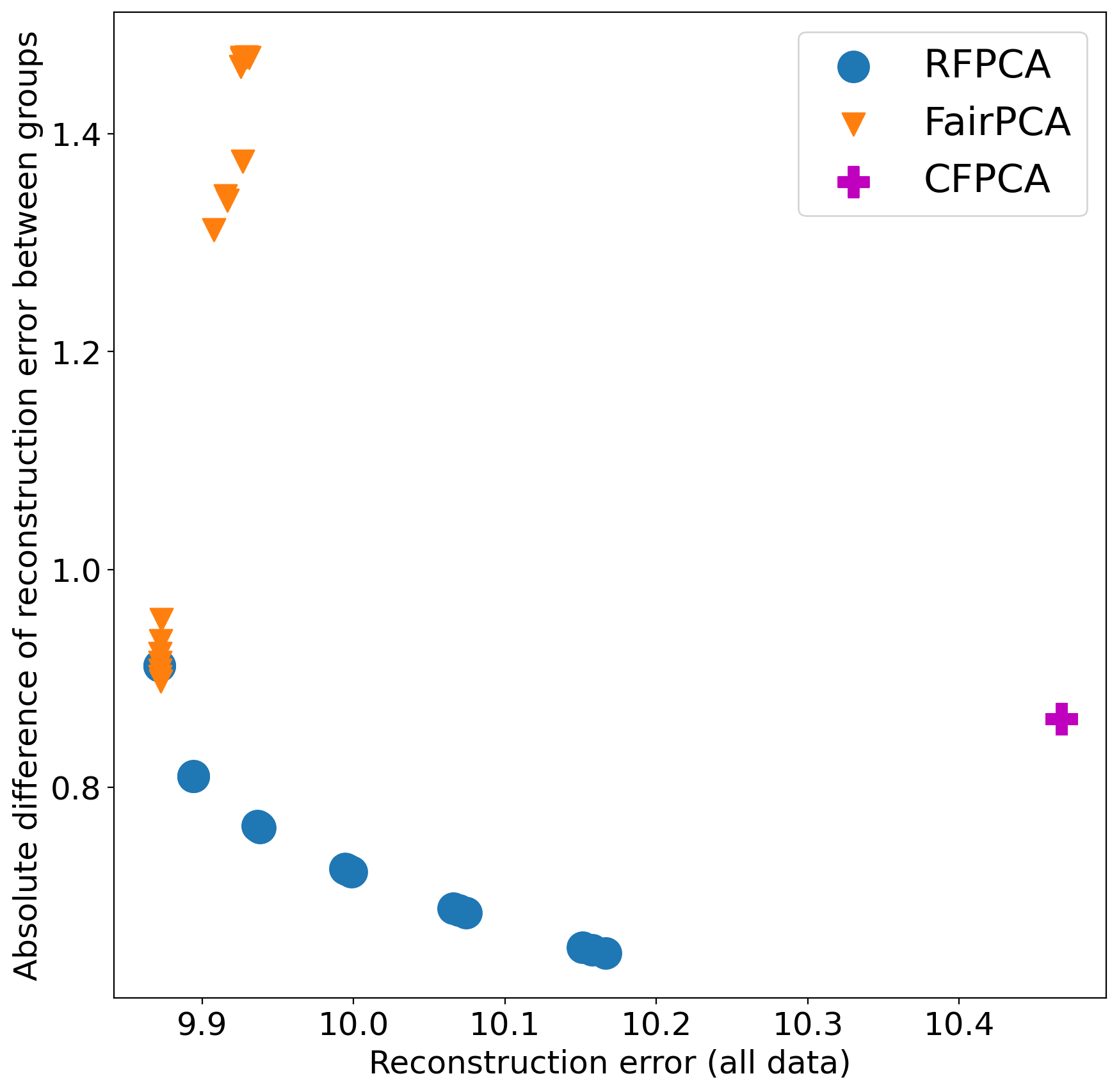
We examine the trade-off between the total reconstruction error and the gap between the subgroups’ reconstruction error. We plot a pareto curve for each of them over the two criteria with different hyper-parameters (hyper-parameters test range are mentioned above). The whole datasets are used for both training and evaluation. The results averaged over 5 runs. The following figure shows the results on the “Default Credit” dataset, with our method having a better pareto curve forms a lower bound to other methods.
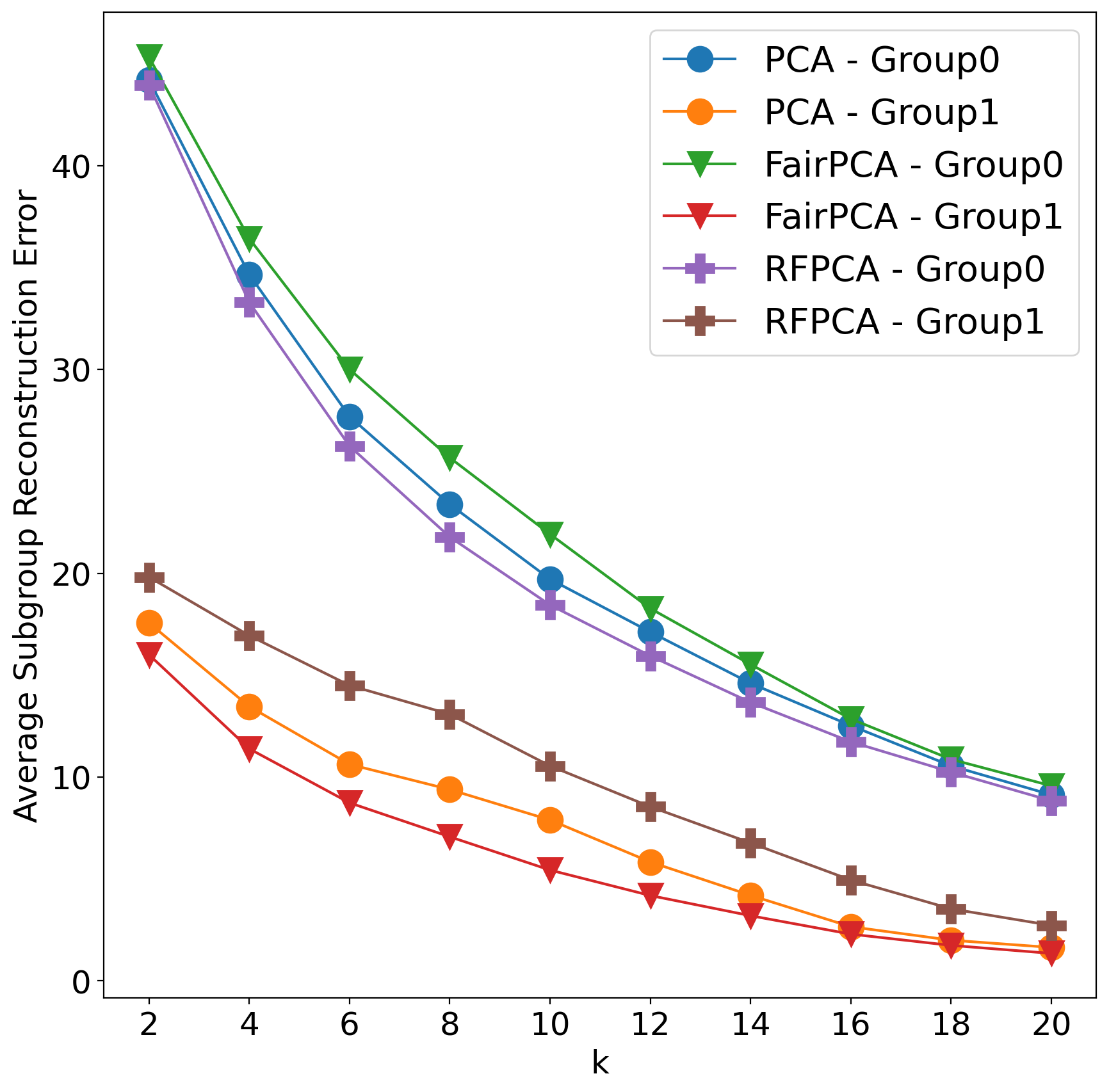
We also show that our method performs well consistently over different numbers of principal components. We first split each dataset into training set and test set with equal size (50% each), the projection matrix of each method is learned from the training set and tested over the test set. The results on the Biodeg dataset is shown in the following figure, our method always provide smaller gap between subgroups’ reconstruction error:
References
Ninareh Mehrabi, Fred Morstatter, Nripsuta Saxena, Kristina Lerman, and Aram Galstyan. A survey on bias and fairness in machine learning. ACM Computing Surveys (CSUR), 54(6):1–35, 2021.
Richard Berk, Hoda Heidari, Shahin Jabbari, Michael Kearns, and Aaron Roth. Fairness in criminal justice risk assessments: The state of the art. Sociological Methods & Research, 50(1):3–44, 2021.
Karl Pearson. Liii. On lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin philosophical magazine and journal of science, 2(11):559–572, 1901.
Harold Hotelling. Analysis of a complex of statistical variables into principal components. Journal of educational psychology, 24(6):417, 1933.
Samira Samadi, Uthaipon Tantipongpipat, Jamie H Morgenstern, Mohit Singh, and Santosh Vempala. The price of fair PCA: One extra dimension. In Advances in Neural Information Processing Systems, pp. 10976–10987, 2018.
Gad Zalcberg and Ami Wiesel. Fair principal component analysis and filter design. IEEE Transactions on Signal Processing, 69:4835–4842, 2021.
Matt Olfat and Anil Aswani. Convex formulations for fair principal component analysis. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 33, pp. 663–670, 2019.
Daniel Kuhn, Peyman Mohajerin Esfahani, Viet Anh Nguyen, and Soroosh Shafieezadeh-Abadeh. Wasserstein distributionally robust optimization: Theory and applications in machine learning. In Operations Research & Management Science in the Age of Analytics, pp. 130–166. INFORMS, 2019.
Hamed Rahimian and Sanjay Mehrotra. Distributionally robust optimization: A review. arXiv preprint arXiv:1908.05659, 2019.
Viet Anh Nguyen, Soroosh Shafieezadeh Abadeh, Man-Chung Yue, Daniel Kuhn, and Wolfram Wiesemann. Calculating optimistic likelihoods using (geodesically) convex optimization. In Advances in Neural Information Processing Systems, pp. 13942–13953, 2019.
Pierre-Antoine Absil, Robert Mahony, and Rodolphe Sepulchre. Optimization Algorithms on Matrix Manifolds. Princeton University Press, 2007.
Xiao Li, Shixiang Chen, Zengde Deng, Qing Qu, Zhihui Zhu, and Anthony Man Cho So. Weakly convex optimization over Stiefel manifold using Riemannian subgradient-type methods. SIAM Journal on Optimization, 33(3):1605–1634, 2021.
Overall
Hieu Vu (Research Resident), Toan Tran and Nguyen Viet Anh (Research Scientist)
Share Article