Viet Nguyen, Giang Vu, Tung Nguyen Thanh, Khoat Than, Toan Tran
Introduction
An autoencoder is a neural network that is trained to attempt to reconstruct its input. Autoencoders are successfully applied to dimensionality reduction and information retrieval tasks. An autoencoder has two components: an encoder mapping an input to a latent code and a decoder mapping a latent code to an output called a reconstruction. The learning process of an autoencoder can be described as minimizing a loss function that penalizes the dissimilarity between inputs and reconstructions. A point cloud is a set of d-dimensional vectors of coordinates, color, normals, etc.
In this work, we try to answer the following question: when learning autoencoders for point clouds, how do different types of loss functions affect the learning process and the quality of latent codes?
Background
We briefly review popular loss functions people use to train autoencoders on point clouds. The first one is Chamfer discrepancy: Given two point clouds P, Q, Chamfer discrepancy between P and Q is defined by
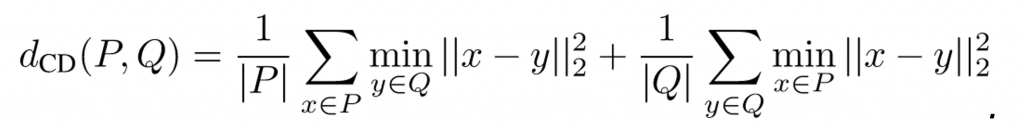 (1)
(1)Another distance used to compare two point clouds is the Earth Mover’s distance (EMD). When P and Q have the same number of points, the EMD between two point clouds P and Q is defined as
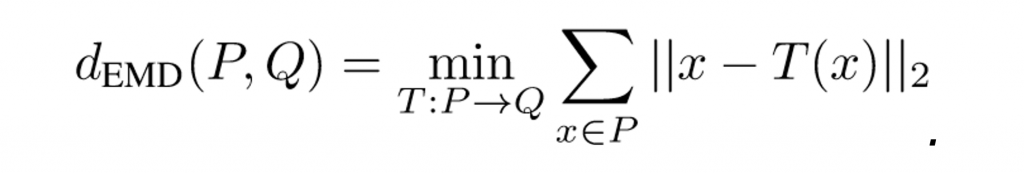
In this work, we also propose to use the Sliced Wasserstein distance (SWD). In particular, the idea of sliced Wasserstein distance is that we first project both target probability measures µ and ν on a direction, says θ, on the unit sphere to obtain two projected measures denoted by πθ#µ and πθ#ν, respectively. Then, we compute the Wasserstein distance between two projected measures πθ#µ and πθ#ν. The sliced Wasserstein distance (SWD) is defined by taking the average of the Wasserstein distance between the two projected measures over all possible projected direction θ. In particular, for any given p ≥ 1, the sliced Wasserstein distance of order p is formulated as follows:
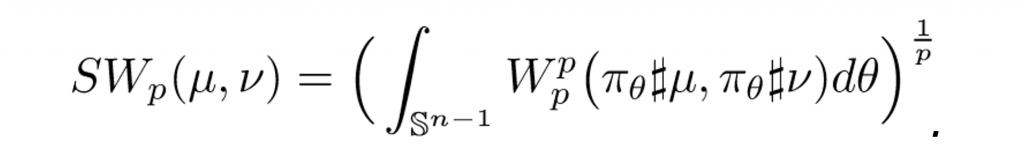
The SWp is considered as a low-cost approximation for Wasserstein distance as its computational complexity is of the order O(nlogn) where n is the maximum number of supports of the discrete probability measures µ and ν. When p = 1, the SWp is weakly equivalent to first order WD or equivalently EMD [1]. The equivalence between SW1 and EMD along with the result of Lemma 1 suggests that SW1 is stronger metric than the Chamfer divergence while it has an appealing optimal computational complexity that is linear on the number of points of point clouds, which is comparable to that of Chamfer divergence.
Findings
Lemma 1. Assume |P| = |Q| and the support of P and Q is bounded in a convex hull of diameter K, then we find that
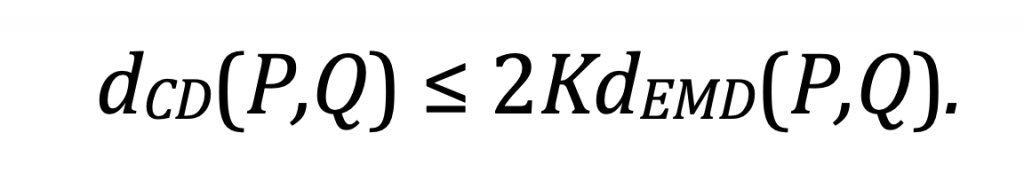
The inequality in Theorem 1 implies that minimizing the Wasserstein distance leads to a smaller Chamfer discrepancy, and the reverse inequality is not true.
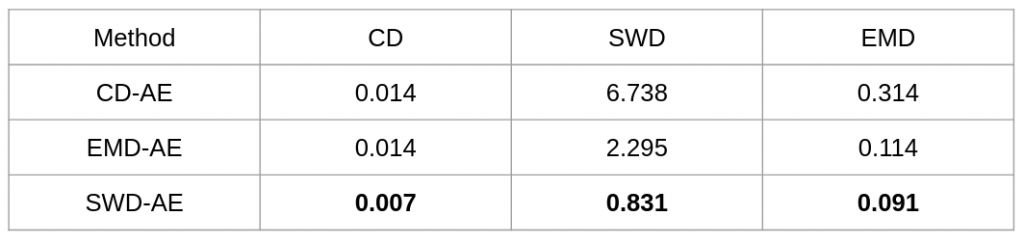
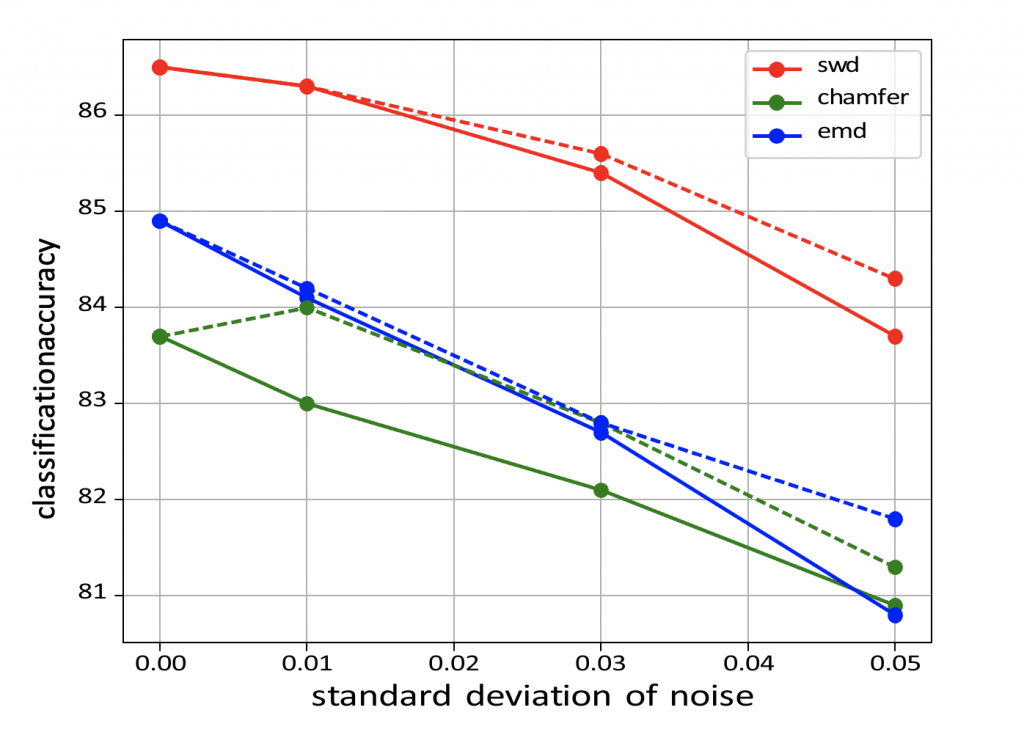
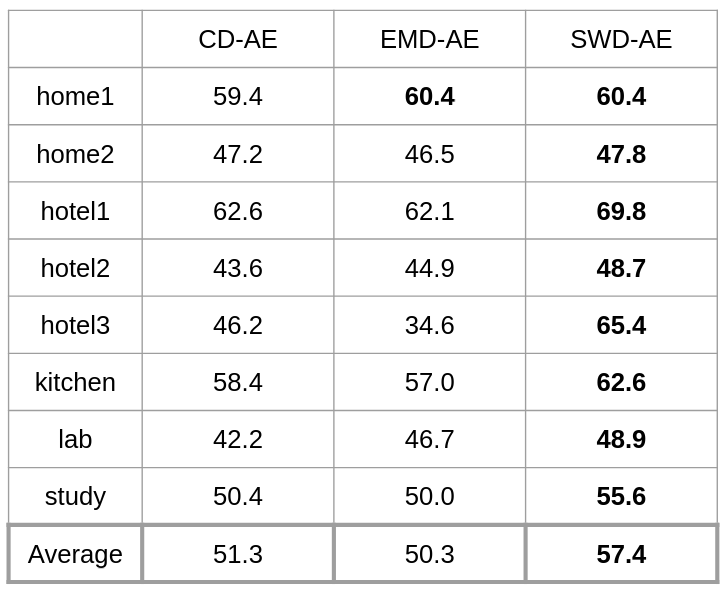
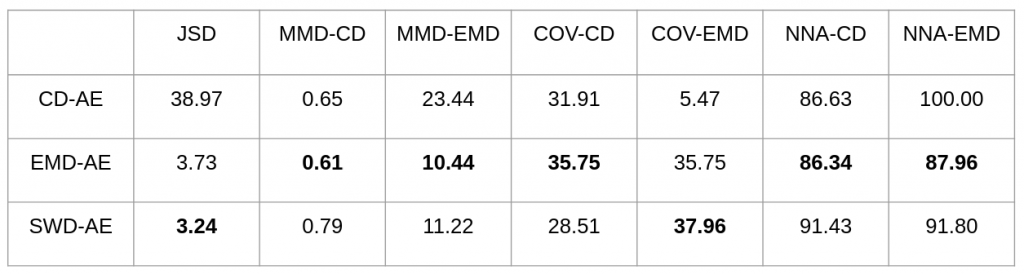
Experiment Results In general, good latent codes are expected to have good performance in a wide range of downstream tasks. Here we compare the performance of different autoencoders trained with Chamfer discrepancy, Earth Mover’s distance, sliced Wasserstein distance. We consider the following tasks in our evaluation: point cloud reconstruction(Table 1), classification(Figure 2), registration(Table 3), and generation(Table 4).
Conclusion
In conclusion, SWD possesses both the statistical benefits of EMD and the computational benefits of Chamfer divergence. Also, latent codes learned by SWD seem to lead to better performance in many downstream tasks than those learned by Chamfer and EMD.
References
[1] Erhan Bayraktar and Gaoyue Guo. Strong equivalence between metrics of Wasserstein type. arXiv preprint arXiv:1912.08247, 2019.
ICCV 2021: Point-set Distances for Learning Representations of 3D Point Clouds
Authors: Trung Nguyen, Quang-Hieu Pham, Tam Le, Tung Pham, Nhat Ho, Binh-Son Hua
Overall
Trung Nguyen (Research Resident)
Share Article




